Answer: 1.960
Explanation:
The value of z we use to calculate a confidence interval with a (
 ) confidence level is a two-tailed test value i.e. represented by :-
) confidence level is a two-tailed test value i.e. represented by :-

Given : The level of confidence:
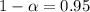
Then, significance level :
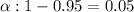
With the help of standard normal distribution table for z , we have
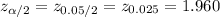
Hence, the value of z should be used to calculate a confidence interval with a 95% confidence level =1.960