Answer:
4.0921 is the logarithm of the equilibrium constant.
Explanation:
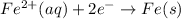 ; E° = - 0.41 V
; E° = - 0.41 V
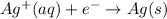 ; E° = 0.80 V
; E° = 0.80 V
Iron having negative value of reduction potential .So ,that means that it will loose electron easily and get oxidized.Hence, will be at anode.
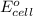 =Reduction potential of cathode - Reduction potential of anode
=Reduction potential of cathode - Reduction potential of anode
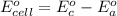
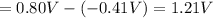
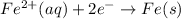 ; E° = - 0.41 V
; E° = - 0.41 V
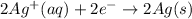 ; E° = 0.80 V
; E° = 0.80 V
Net reaction:
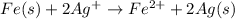
n = 2
To calculate equilibrium constant, we use the relation between Gibbs free energy, which is:

and,
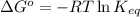
Equating these two equations, we get:
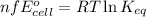
where,
n = number of electrons transferred = 2
F = Faraday's constant = 96500 C
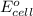 = standard electrode potential of the cell = 1.21 V
= standard electrode potential of the cell = 1.21 V
R = Gas constant = 8.314 J/K.mol
T = temperature of the reaction =
![25^oC=[273+25]=298K](https://img.qammunity.org/2020/formulas/chemistry/college/6emvaajqo5qvucrhq2qn2dbo2gul9o60b4.png)
Putting values in above equation, we get:
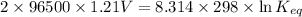
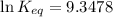
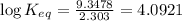
4.0921 is the logarithm of the equilibrium constant.