Question

What is the logarithm of the equilibrium constant, log K, at 25°C of the voltaic cell constructed from the following two half-reactions? Fe2+ (aq) + 2e¯ Fe(s); ​E​° = – 0.41V Ag+(aq) + e–Ag(s); E° = 0.80 V

Answer 1

4.0921 is the logarithm of the equilibrium constant.

Explanation:

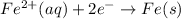`Fe^(2+) (aq) +2e^(-)\rightarrow Fe(s)`; ​E​° = - 0.41 V

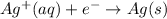`Ag^+(aq) + e^-\rightarrow Ag(s)`; E° = 0.80 V

Iron having negative value of reduction potential .So ,that means that it will loose electron easily and get oxidized.Hence, will be at anode.

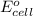`E^(o)_(cell)`=Reduction potential of cathode - Reduction potential of anode

`E^(o)_(cell)=E^(o)_c-E^(o)_a`

`=0.80 V-(-0.41 V)=1.21 V`

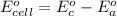
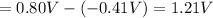
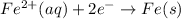`Fe^(2+) (aq) + 2e^(-)\rightarrow Fe(s)`; ​E​° = - 0.41 V

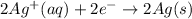`2Ag^+(aq) + 2e^-\rightarrow 2Ag(s)`; E° = 0.80 V

Net reaction:
`Fe(s)+2Ag^(+)\rightarrow Fe^(2+)+2Ag(s)`

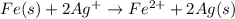
n = 2

To calculate equilibrium constant, we use the relation between Gibbs free energy, which is:

`\Delta G^o=-nfE^o_(cell)`

and,

`\Delta G^o=-RT\ln K_(eq)`

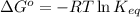
Equating these two equations, we get:

`nfE^o_(cell)=RT\ln K_(eq)`

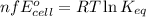
where,

n = number of electrons transferred = 2

F = Faraday's constant = 96500 C

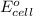`E^o_(cell)` = standard electrode potential of the cell = 1.21 V

R = Gas constant = 8.314 J/K.mol

T = temperature of the reaction =
`25^oC=[273+25]=298K`

Putting values in above equation, we get:

`2* 96500* 1.21 V=8.314* 298* \ln K_(eq)`

`\ln K_(eq)=9.3478`

`\log K_(eq)=(9.3478)/(2.303)=4.0921`

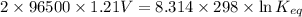
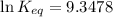
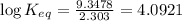
4.0921 is the logarithm of the equilibrium constant.