Question

In the manufacturing process of sulfuric acid, sulfur dioxide is reacted with oxygen to produce sulfur trioxide. Using the equation, 2SO2 (g) + O2 Imported Asset 2SO3 (g), if 64.06g of sulfur dioxide is given an opportunity to react with an excess of oxygen to produce 75.00 g of sulfur trioxide, what is the percent yield of this reaction? 46.83% 60.25% 75.55% 93.68%

Answer 1

Answer:do you still need help ?

Step-by-step explanation:

Answer 2

Answer : The percent yield of the reaction is, 93.68 %

Explanation : Given,

Mass of
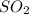`SO_2` = 64.06 g

Molar mass of
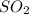`SO_2` = 64 g/mole

Molar mass of
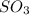`SO_3` = 80 g/mole

First we have to calculate the moles of
`SO_2`.

`\text{Moles of }SO_2=\frac{\text{Mass of }SO_2}{\text{Molar mass of }SO_2}=(64.06g)/(64g/mole)=1.0009mole`

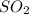Now we have to calculate the moles of
`SO_3`.

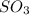The balanced chemical reaction will be,

`2SO_2+O_2\rightarrow 2SO_3`

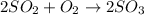
From the balanced reaction, we conclude that

As, 2 moles of
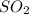`SO_2` react to give 2 moles of
`SO_3`

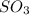
So, 1.0009 moles of
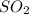`SO_2` react to give 1.0009 moles of
`SO_3`

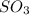
Now we have to calculate the mass of
`SO_3`

`\text{Mass of }SO_3=\text{Moles of }SO_3* \text{Molar mass of }SO_3`

`\text{Mass of }SO_3=(1.0009mole)* (80g/mole)=80.072g`

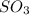
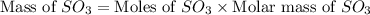
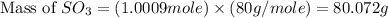
The theoretical yield of
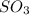`SO_3` = 80.072 g

The actual yield of
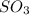`SO_3` = 75.00 g

Now we have to calculate the percent yield of
`SO_3`

`\%\text{ yield of the reaction}=\frac{\text{Actual yield of }SO_3}{\text{Theoretical yield of }SO_3}* 100=(75.00g)/(80.072g)* 100=93.68\%`

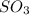
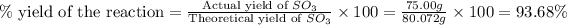
Therefore, the percent yield of the reaction is, 93.68 %