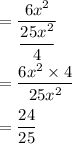Answer:
The ratio of the area of region R to the area of region S is:
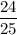
Explanation:
The sides of R are in the ratio : 2:3
Let the length of R be: 2x
and the width of R be: 3x
i.e. The perimeter of R is given by:
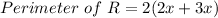
( Since, the perimeter of a rectangle with length L and breadth or width B is given by:
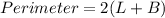 )
)
Hence, we get:
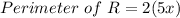
i.e.
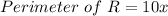
Also, let " s " denote the side of the square region.
We know that the perimeter of a square with side " s " is given by:

Now, it is given that:
The perimeters of square region S and rectangular region R are equal.
i.e.
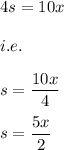
Now, we know that the area of a square is given by:

and
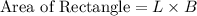
Hence, we get:
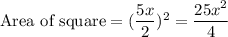
and
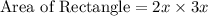
i.e.
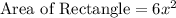
Hence,
Ratio of the area of region R to the area of region S is: