Answer:
The perimeter of the rectangle B C E F is 16.97 units
Explanation:
* Lets explain how to solve the problem
- B C E F is a rectangle
- The perimeter of the rectangle is the sum of the length of its
four sides
- The coordinates of the vertices of the rectangle are:
B (0 , 3) , C (4 , -1) , E (2 , -3) , F (-2 , 1)
- To find the dimensions of the rectangle use the rule of distance
d =
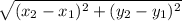
* Lets solve the problem
∵
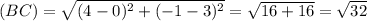
∵
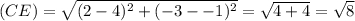
∵

∵
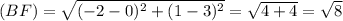
∵ The perimeter of the rectangle = BC + CE + FE + BF
∴ The perimeter =
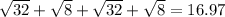
∴ The perimeter of the rectangle B C E F is 16.97 units