Question

Find the perimeter of rectangle BCEF. Round your answer to the nearest hundredth

A(-5, 4)
B(0, 3)
F(-2, 1)
-4 -2
6
x
C(4, -1)
1
E(2, -3)
D(4, -5)

Answer 1

The perimeter of the rectangle B C E F is 16.97 units

Explanation:

* Lets explain how to solve the problem

- B C E F is a rectangle

- The perimeter of the rectangle is the sum of the length of its

four sides

- The coordinates of the vertices of the rectangle are:

B (0 , 3) , C (4 , -1) , E (2 , -3) , F (-2 , 1)

- To find the dimensions of the rectangle use the rule of distance

d =
`\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

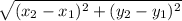
* Lets solve the problem

∵
`(BC)=\sqrt{(4-0)^(2)+(-1-3)^(2)}=√(16+16)=√(32)`

∵
`(CE)=\sqrt{(2-4)^(2)+(-3--1)^(2)}=√(4+4)=√(8)`

∵
`(FE)=\sqrt{(2--2)^(2)+(-3-1)^(2)}=√(16+16)=√(32)`

∵
`(BF)=\sqrt{(-2-0)^(2)+(1-3)^(2)}=√(4+4)=√(8)`

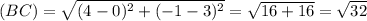
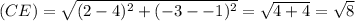
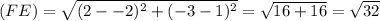
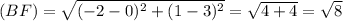
∵ The perimeter of the rectangle = BC + CE + FE + BF

∴ The perimeter =
`√(32)+√(8)+√(32)+√(8)=16.97`

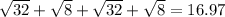
∴ The perimeter of the rectangle B C E F is 16.97 units