Answer:
Lowest Current : c=0 and 6 Amp
Highest Current : 3 amp
Explanation:
We are given our function as
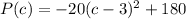
We are asked to determine the values of current c at which the power P(c) is equal to 0
Hence
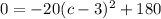
Now we solve the above equation for c
subtracting 180 from each side we get
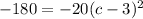
Dividing both sides by -20
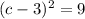
Taking square root on both sides
c-3= ±3
adding 3 on both sides
c=±3+3
hence
c= 0
or
c=6
At c=0 and 6 amperes the power will be minimum
Now we have to find the c at which the power will be the highest
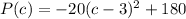
Represents a parabola
subtracting 180 from both sides we get
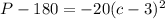
Comparing it with standard parabola

(h,k) will be the coordinates of the vertex
Hence here
h=3 , k = 180
Hence in this equation
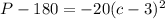
The vertex will be (3,180)
Or at c=3, P = 180 the maximum