Question

The power generated by an electrical circuit (in watts) as a function of its current ccc (in amperes) is modeled by:

P(c)=−20(c−3)^2 + 180

Which currents will produce no power (i.e. 000 watts)?
Enter the lower current first.

Lower current: _______ amperes
Higher current: _______amperes

Answer 1

lower 0

higher 6

Explanation:

Answer 2

Lowest Current : c=0 and 6 Amp

Highest Current : 3 amp

Explanation:

We are given our function as

`P(c)=-20(c-3)^2 + 180`

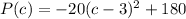
We are asked to determine the values of current c at which the power P(c) is equal to 0

Hence

`0=-20(c-3)^2+ 180`

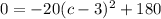
Now we solve the above equation for c

subtracting 180 from each side we get

`-180=-20(c-3)^2`

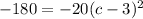
Dividing both sides by -20

`(c-3)^2=9`

Taking square root on both sides

c-3= ±3

adding 3 on both sides

c=±3+3

hence

c= 0

or

c=6

At c=0 and 6 amperes the power will be minimum

Now we have to find the c at which the power will be the highest

`P(c)=-20(c-3)^2+ 180`

Represents a parabola

subtracting 180 from both sides we get

`P-180=-20(c-3)^2`

Comparing it with standard parabola

`(y-k)^2=-4k(x-h)^2`

(h,k) will be the coordinates of the vertex

Hence here

h=3 , k = 180

Hence in this equation
`P-180=-20(c-3)^2`

The vertex will be (3,180)

Or at c=3, P = 180 the maximum