Answers:
a)
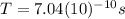
b)
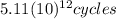
c)
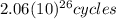
d) 46000 s
Step-by-step explanation:
a) Time for one cycle of the radio wave
We know the maser radiowave has a frequency
 of
of
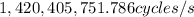
In addition we know there is an inverse relation between frequency and time
 :
:
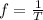 (1)
(1)
Isolating
 :
:
 (2)
(2)
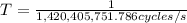 (3)
(3)
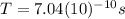 (4) This is the time for 1 cycle
(4) This is the time for 1 cycle
b) Cycles that occur in 1 h
If
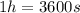 and we already know the amount of cycles per second
and we already know the amount of cycles per second
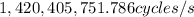 , then:
, then:
 This is the number of cycles in an hour
This is the number of cycles in an hour
c) How many cycles would have occurred during the age of the earth, which is estimated to be
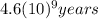 ?
?
Firstly, we have to convert this from years to seconds:
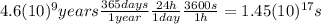
Now we have to multiply this value for the frequency of the maser radiowave:
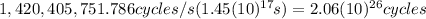 This is the number of cycles in the age of the Earth
This is the number of cycles in the age of the Earth
d) By how many seconds would a hydrogen maser clock be off after a time interval equal to the age of the earth?
If we have 1 second out for every 100,000 years, then:
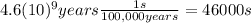
This means the maser would be 46000 s off after a time interval equal to the age of the earth