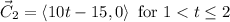Question

Find an appropriate parametrization for the given piecewise-smooth curve in R^2, with the implied orientation. The curve C, which goes along the circle of radius 5, from the point (5, 0) above the x-axis to the point (-5, 0), and then in a straight line along the x-axis back to (5, 0). circle portion C_1(t) = for 0 lessthanorequalto t lessthanorequalto 1 line portion C_2(t) = for 1 < t lessthanorequalto 2

Answer 1

`\vec{C}_1(t)=\displaystyle\left<5\cos(\pi t), 5\sin(\pi t) \right> \text{ for }0\le t\le 1`

`\vec{C}_2(t)=\displaystyle\left<10t-15, 0 \right> \text{ for }1 < t\le 2`

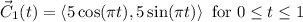
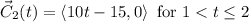
Step by step explanation:

To help visualize see the attached graph.

The semicircle can be parametrized by using the standard polar formulas:

`x=r\cos(s), y=r\sin(s), \text{ for }0\le s\le \pi`

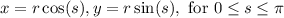
Where r is the radius of the circle, therefore r=5.

Nevertheless, since we want a parameter t starting at 0 and ending at 1, notice we need to adjust the parameter s. So, we need that:

`\text{When }t=0\to s=0\\\text{When }t=1\to s=\pi\\`

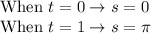
We can achieve that by setting:

`s=\displaystyle\pi t`

Therefore, the parametrization of the semicircle becomes:

`\displaystyle x=5\cos(\pi t), y=5\sin(\pi t), \text{ for }0\le t\le 1`

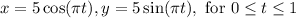
In vector form:

`\vec{C}_1(t)=\displaystyle \left<5\cos(\pi t), 5\sin(\pi t) \right> \text{ for }0\le t\le 1`

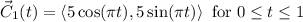
Then for the segment of line, y remains 0 since we are moving along the x-axis. So, y=0

While x increases from -5 to 5. When t=1, x =-5, and when t=2, x=5. It is like finding the equation of a line with ordered pairs (t, x): (1, -5) and (2, 5). Whose slope is therefore: 10. Then using the point-slope formula:

`x-x_1=m(t-t_1)`

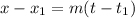
And plugging the slope and one of the points we get:

`x-5=10(t-2)\to x=10t-15`

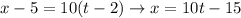
So, now we can build our parametrization for the segment of line:

`\vec{C}_2=\displaystyle\left<10t-15, 0 \right> \text{ for }1 < t\le 2`