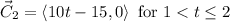Answer:
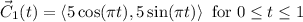
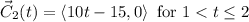
Step by step explanation:
To help visualize see the attached graph.
The semicircle can be parametrized by using the standard polar formulas:
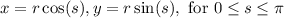
Where r is the radius of the circle, therefore r=5.
Nevertheless, since we want a parameter t starting at 0 and ending at 1, notice we need to adjust the parameter s. So, we need that:
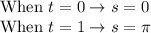
We can achieve that by setting:

Therefore, the parametrization of the semicircle becomes:
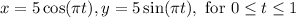
In vector form:
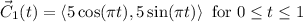
Then for the segment of line, y remains 0 since we are moving along the x-axis. So, y=0
While x increases from -5 to 5. When t=1, x =-5, and when t=2, x=5. It is like finding the equation of a line with ordered pairs (t, x): (1, -5) and (2, 5). Whose slope is therefore: 10. Then using the point-slope formula:
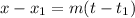
And plugging the slope and one of the points we get:
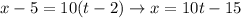
So, now we can build our parametrization for the segment of line: