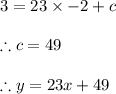Question

Suppose for a function y = f(x) that f(-2) = 3 and f'(-2) = 23 . Write the equation of the tangent line to f(x) at x = -2.

Answer 1

The equation of tangent line is
`y=23x+49`.

Explanation:

Given information: y = f(x) that f(-2) = 3 and f'(-2) = 23 .

The given function is

`y=f(x)`

Differentiate with respect to x.

`y'=f'(x)`

We need to find the equation of the tangent line to f(x) at x = -2.

Slope of tangent line is

`y'_([x=-2])=f'(-2)=23`

Slope of line is 23.

At x=-2 the value of function is 3. It means the tangent line passes through the point (-2,3).

Equation of tangent line is

`y-y_1=m(x-x_1)`

`y-3=23(x-(-2))`

`y-3=23x+46`

Add 3 on both sides.

`y=23x+49`

Therefore the equation of tangent line is
`y=23x+49`.

Answer 2

The equation of the line is
`y=23x+49`

Explanation:

The general equation of a line is given by

`y=mx+c`

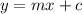
Where,

'm' is the slope of the line

'c' is the intercept of the line

Now we are given that
`f'(x)|_(x=-2)=23`

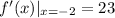
By definition the derivative of a function at any point is the slope of the tangent at that point

Thus the slope of the line passing x = -2 is 23

Hence 'm' = 23

Thus the equation of the line becomes

`y=23x+c`

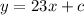
to find the intercept we are given that the line passes through (-2,3)

Using this information in the above equation of line we get

`3=23* -2+c\\\\\therefore c=49\\\\\therefore y=23x+49`