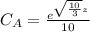Question

Compound A, with concentration CA, diffuses through a 4-cm long tube and reacts as it diffuses. The equation governing diffusion with reaction is given by D d 2CA dz2 − kCA = 0 (7) At one end of the tube, there is a large source of A at a concentration of CA=0.1M. At the other end of the tube there is an adsorbent material that quickly absorbs any A, making the concentration 0 M. If D =1.5×10−6 cm2/s and k =5×10−6 s −1 , what is the concentration of A as a function of distance in the tube

Answer 1

`C_(A)=\frac{e^{\sqrt{(10)/(3) }z}}{10}`

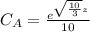
Explanation:

First you need to rearrange the original equation in order to have an equation with a general form:

`D (d^(2)C_(A))/(d^(2)z) -kC_(A)=0`

We divide everything by D, so we have:

`(d^(2)C_(A))/(d^(2)z) -(k)/(D) C_(A)=0`

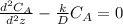
We know that k and D are constants, so we can leave them as just one constant that gives as result:

`(10)/(3) =(k)/(D)`

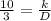
Then we proceed to change terms in the equation son it looks friendlier:

`y''-(10)/(3)y=0`

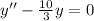
Knowing that
`y=C_(A)`

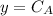
Then we give the general solution for the differential equation of second order:

`y=C_(1)e^{\sqrt{(10)/(3) } z} + C_(2)e^{-\sqrt{(10)/(3) } z}`

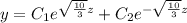
The following is knowing the frontier values so we can calculate the constants of the equation:

`z=0; y=0.1\\z=z; y=0`

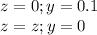
With these values, we can replace in the general solution to find the final equation:

`0.1=C_(1)e^{\sqrt{(10)/(3) }0} + C_(2)e^{-\sqrt{(10)/(3) }0}\\0.1=C_(1) + C_(2)`

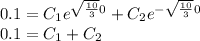
And with the other values:

`0=C_(1)e^{\sqrt{(10)/(3) }z} + C_(2)e^{-\sqrt{(10)/(3) }z}`

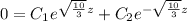
Then we solve the equation system, as we have two unknowns, the constants, and two equations:

`C_(1)=0.1-C_(2)\\0=(0.1-C_(2))e^{\sqrt{(10)/(3) }z} +C_(2)e^{-\sqrt{(10)/(3) }z}`

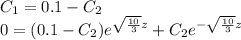
After solving both equations, we have;
`C_(A)=\frac{e^{\sqrt{(10)/(3) } z}}{10}((1-\frac{e^{\sqrt{(10)/(3) }z}}{{-e^{\sqrt{(10)/(3) }z}}+{e^{-\sqrt{(10)/(3) }z}}} ) + (\frac{e^{\sqrt{(10)/(3) }z}}{{-e^{\sqrt{(10)/(3) }z}}+{e^{-\sqrt{(10)/(3) }z}}}))`

The we see that we can cancel terms, so we have the final solution that is:

`C_(A)=\frac{e^{\sqrt{(10)/(3) }z}}{10}`