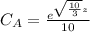Answer:
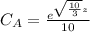
Explanation:
First you need to rearrange the original equation in order to have an equation with a general form:
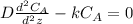
We divide everything by D, so we have:
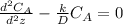
We know that k and D are constants, so we can leave them as just one constant that gives as result:
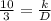
Then we proceed to change terms in the equation son it looks friendlier:
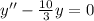
Knowing that
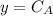
Then we give the general solution for the differential equation of second order:
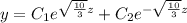
The following is knowing the frontier values so we can calculate the constants of the equation:
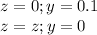
With these values, we can replace in the general solution to find the final equation:
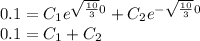
And with the other values:
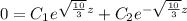
Then we solve the equation system, as we have two unknowns, the constants, and two equations:
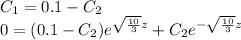
After solving both equations, we have;
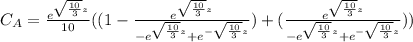
The we see that we can cancel terms, so we have the final solution that is: