Question

In guinea pigs hair straightness or curliness is thought to be governed by a single pair of alleles showing incomplete dominance. Individuals with straight hair are homozygous for the S allele, those with curly hair are homozygous for the C allele, and individuals with wavy hair are heterozygous (SC). You collect data on 1,000 individuals from a population and discover that 244 have straight hair, 444 have curly hair, and 312 have wavy hair.a) Calculate the allele frequencies of the S and C alleles.b.) Is this population in Hardy-Weinberg equilibrium? Show work to support your answer.

Answer 1

Frequency of allele S is p
`= 0.4939`

Frequency of allele C is q
`= 0.666`

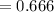
The population is not in Hardy-Weinberg equilibrium

Step-by-step explanation:

Given -

Number of individuals with straight hair
`= 244`

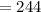
Number of individuals with curly hair
`= 444`

Number of individuals with Wavy hair
`= 312`

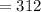
Let "p" represents the frequency for allele for straight hair and "q" represents the frequency for allele for curly hair

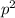`p^2` represents the frequency of genotype "SS"

`p^(2) = (244)/(1000) \\= 0.244`

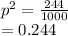
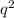`q^2` represents the frequency of genotype "CC"

`p^(2) = (444)/(1000) \\= 0.444`

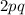`2pq` represents the frequency of genotype "SC"

`2pq = (312)/(1000) \\= 0.312`

Frequency of allele S is p

`= √(0.244) \\= 0.4939`

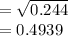
Frequency of allele C is q

tex]= \sqrt{0.444} \\= 0.666[/tex]

For being in Hardy Weinberg's equation-

`p+q=1\\`

Substituting the values in above equation, we get -

`0.4939+0.666\\eq 1`

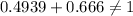
hence, the population is not in Hardy-Weinberg equilibrium