Question

A 36.3 mL aliquot (sample) of 0.529 M H2SO4 (aq) is to be titrated with 0.0411 M NaOH. What volume of base will it take to reach the equivalence point?

Answer 1

Answer: 934.4 ml

Step-by-step explanation:

According to the neutralization law,

`n_1M_1V_1=n_2M_2V_2`

where,

`M_1` = molarity of
`H_2SO_4` solution = 0.529 M

`V_1` = volume of
`H_2SO_4` solution = 36.3 ml

`M_2` = molarity of
`NaOH` solution = 0.0411 M

`V_2` = volume of
`NaOH` solution = ?

`n_1` = valency of
`H_2SO_4` = 2

`n_2` = valency of
`NaOH` = 1

`2* 0.529M* 36.3=1* 0.0411* V_2`

`V_2=934.4ml`

Therefore, the volume of the base required to reach the equivalence point is 934.4 ml

Answer 2

Step-by-step explanation:

Sulfuric acid (
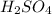`H_(2)SO_(4)`) is a diprotic acid. So, it means that we need twice as much NaOH.

As we known that an equivalence point is reached when moles of an acid equals the moles of a base.

As moles of
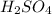`H_(2)SO_(4)` is calculated as follows.

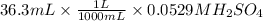`36.3 mL * (1 L)/(1000 mL) *  0.0529 M H_(2)SO_(4)` = 0.00192 moles of
`H_(2)SO_(4)`

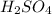
Therefore, moles of NaOH needed will be as follows.

`2 * 0.00192 moles`

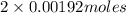
= 0.00384 mol

Hence, volume of NaOH is calculated as follows.

`(1000 mL)/(1 L) * (0.00384 moles)/(0.0411 M NaOH)`

= 93.43 mL

Thus, we can conclude that the volume of base required to reach the equivalence point is 93.43 mL.