Answer: Option A
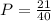
Explanation:
Bag (1)
white marbles: 3
black marbles: 5
total marbles: 8
Probability of taking out a white marble
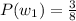
Probability of taking out a black marble

Bag (2)
white marbles: 4
black marbles: 6
total marbles: 10
Probability of taking out a white marble
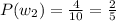
Probability of taking out a black marble

Note that the events are independent. The marble that you take out in the second bag does not depend on the one you took out in the first bag
You can draw two white marbles or two black marbles
white, white or black, black
Then the probability that both marbles are of the same color is:
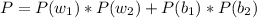
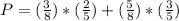
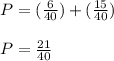
The answer is the option A