Question

One bag contains three white marbles and five black marbles, and a second bag contains four white marbles and six black marbles. A person draws one marble from each bag. Find the probability that both marbles are of the same color.

A.)21/40
B.)1/2
C.)3/14

Answer 1

There are two possible ways of getting 2 of the same color.
The chance of getting two white ones is 3/8 times 4/10 which is 0.15
The chance of getting two black ones is 5/8 times 6/10 which is 0.375
0.15+0.375=0.525 which is 21/40

So the answer is A.) 21/40

Answer 2

Answer: Option A

`P=(21)/(40)`

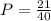
Explanation:

Bag (1)

white marbles: 3

black marbles: 5

total marbles: 8

Probability of taking out a white marble
`P(w_1) = (3)/(8)`

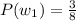
Probability of taking out a black marble
`P(b_1) = (5)/(8)`

Bag (2)

white marbles: 4

black marbles: 6

total marbles: 10

Probability of taking out a white marble
`P(w_2) = (4)/(10)=(2)/(5)`

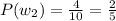
Probability of taking out a black marble
`P(b_2) = (6)/(10)=(3)/(5)`

Note that the events are independent. The marble that you take out in the second bag does not depend on the one you took out in the first bag

You can draw two white marbles or two black marbles

white, white or black, black

Then the probability that both marbles are of the same color is:

`P=P(w_1)*P(w_2) + P(b_1)*P(b_2)`

`P=((3)/(8))*((2)/(5)) + ((5)/(8))*((3)/(5))`

`P=((6)/(40)) + ((15)/(40))\\\\P=(21)/(40)`

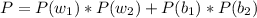
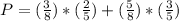
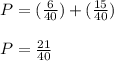
The answer is the option A