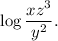Answer: The required condensed expression is
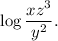
Step-by-step explanation: We are given to fully condense the following logarithmic expression assuming that all variables represent positive numbers :

We will be using the following properties of logarithms :
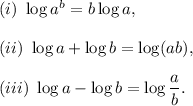
Therefore, from expression (i), we get

Thus, the required condensed expression is