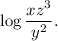Question

Fully condense the expression. Assume that all variables represent positive numbers. (log x -2 log y+ 3 log z) (10 points)

Answer 1

Answer: The required condensed expression is
`\log(xz^3)/(y^2).`

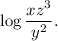
Step-by-step explanation: We are given to fully condense the following logarithmic expression assuming that all variables represent positive numbers :

`E=\log x-2\log y+3\log z~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We will be using the following properties of logarithms :

`(i)~\log a^b=b\log a,\\\\(ii)~\log a+\log b=\log(ab),\\\\(iii)~\log a-\log b=\log(a)/(b).`

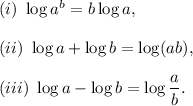
Therefore, from expression (i), we get

`E\\\\=\log x-2\log y+3\log z\\\\=\log x-\log y^2+\log z^3\\\\=\log(xz^3)-\log y^2\\\\=\log(xz^3)/(y^2).`

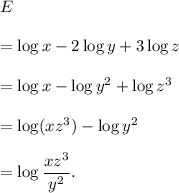
Thus, the required condensed expression is
`\log(xz^3)/(y^2).`