Question

A quadrilateral is graphed on a coordinate plane. If the vertices are A(2, 6), B(6, 0), C(2, –6) and D(–4, 0), which two points are farthest apart?

Answer 1

Check the picture below.

Answer 2

Answer: A(2, 6) and C(2, -6)

Explanation:

The distance between any two points is given by :-

`d=√((d-b)^2+(c-a)^2)`

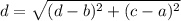
Given vertices : A(2, 6), B(6, 0), C(2, -6) and D(-4, 0)

Then,

`AB=√((0-6)^2+(6-2)^2)=√((-6)^2+(4)^2)=√(36+16)\\\\=√(52)\approx7.211`

`BC=√((-6-0)^2+(2-6)^2)=√((-6)^2+(-4)^2)=√(36+16)\\\\=√(52)\approx7.211`

`CD=√((0-(-6))^2+(-4-2)^2)=√((6)^2+(-6)^2)=√(36+36)\\\\=√(72)\approx8.485`

`AD=√((0-2)^2+(-4-6)^2)=√((-2)^2+(-10)^2)=√(4+100)\\\\=√(104)\approx10.198`

`AC=√((-6-6)^2+(2-2)^2)=√((-12)^2)=√(144)\\\\=\12`

`BD=√((0-0)^2+(-4-6)^2)=√((-10)^2)=√(100)\\\\=10`

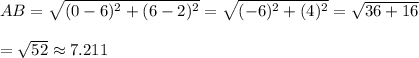
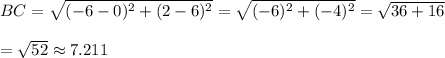
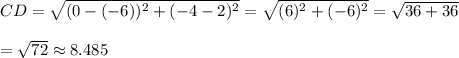
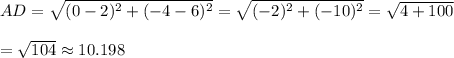
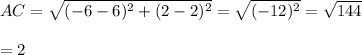
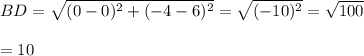
Since, points A and C has the largest distance between them.

Therefore, the points A and C are the farthest points.