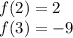For this case we have the following function:
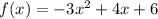
We must evaluate the function when
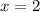 and
and
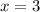
For
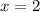 :
:
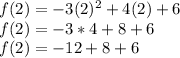
Different signs are subtracted and the major sign is placed.
Equal signs are added and the same sign is placed.
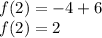
For
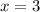 :
:

Different signs are subtracted and the major sign is placed.
Equal signs are added and the same sign is placed.
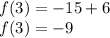
Answer: