Question

Mean, Median, Mode, and Range (A)

Instructions: Calculate the mean, median, mode, and range of each set of numbers. (4 points each exercise)

{218, 365, 461, 512, 595, 595, 690, 739, 836, 836, 836, 896, 896, 954, 954}

Result

Calculation

Mean

Median

Mode

Range

{198, 212, 262, 284, 313, 488, 602, 602, 606, 616, 616, 678, 754, 937, 997}

Result

Calculation

Mean

Median

Mode

Range

{199, 504, 584, 677, 690, 709, 740, 740, 805, 836, 839, 839, 873, 987, 994}

Result

Calculation

Mean

Median

Mode

Range

{136, 238, 320, 403, 434, 553, 555, 571, 571, 581, 723, 824, 857, 948, 971}

Result

Calculation

Mean

Median

Mode

Range

{208, 226, 323, 433, 433, 489, 574, 594, 599, 803, 803, 803, 875, 951, 969}

Result

Calculation

Mean

Median

Mode

Range

Answer 1

1. {198, 212, 262, 284, 313, 488, 602, 602, 606, 616, 616, 678, 754, 937, 997}

Mean of given numbers is:

`Mean = (Sum of all observations)/(Total number of observation)`

`=(218+365+ 461+ 512+ 595+ 595+ 690+ 739+ 836+ 836+ 836+ 896+ 896+ 954+ 954)/(15)`

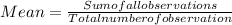
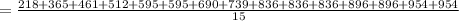
= 692.2

For finding Median, firstly we arrange data in ascending or descending order: 218, 365, 461, 512, 595, 595, 690, 739, 836, 836, 836, 896, 896, 954, 954

Here number of terms is 15 which is odd.

So, Median = { (n + 1) ÷ 2 }th term

= { (15 + 1) ÷ 2 }th term

=
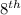`8^(th)` term

= 739

For finding mode, We see the observation that has maximum number of frequency.

Here 836 is repeated 3 times and its frequency is maximum.

So, Mode = 836

Range = Highest value - Lowest value

= 954 - 218

= 736

2. {198, 212, 262, 284, 313, 488, 602, 602, 606, 616, 616, 678, 754, 937, 997}

Mean of given numbers is:

`Mean = (Sum of all observations)/(Total number of observation)`

`=(198+ 212+ 262+ 284+ 313+ 488+ 602+ 602+ 606+ 616+ 616+ 678+ 754+ 937+ 997)/(15)`

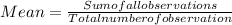
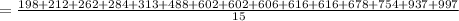
= 544.333

For finding Median, firstly we arrange data in ascending or descending order: 198, 212, 262, 284, 313, 488, 602, 602, 606, 616, 616, 678, 754, 937, 997

Here number of terms is 15 which is odd.

So, Median = { (n + 1) ÷ 2 }th term

= { (15 + 1) ÷ 2 }th term

=
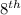`8^(th)` term

= 602

For finding mode, We see the observation that has maximum number of frequency.

Here 616 is repeated 2 times and its frequency is maximum.

So, Mode = 616

Range = Highest value - Lowest value

= 997 - 198

= 799

3. {199, 504, 584, 677, 690, 709, 740, 740, 805, 836, 839, 839, 873, 987, 994}

Mean of given numbers is:

`Mean = (Sum of all observations)/(Total number of observation)`

`=(199+ 504+ 584+ 677+ 690+ 709+ 740+ 740+ 805+ 836+ 839+ 839+ 873+ 987+ 994)/(15)`

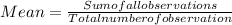
= 734.4

For finding Median, firstly we arrange data in ascending or descending order: 199, 504, 584, 677, 690, 709, 740, 740, 805, 836, 839, 839, 873, 987, 994

Here number of terms is 15 which is odd.

So, Median = { (n + 1) ÷ 2 }th term

= { (15 + 1) ÷ 2 }th term

=
`8^(th)` term

= 740

For finding mode, We see the observation that has maximum number of frequency.

Here 839 is repeated 2 times and its frequency is maximum.

So, Mode = 839

Range = Highest value - Lowest value

= 994 - 199

= 795

4. {136, 238, 320, 403, 434, 553, 555, 571, 571, 581, 723, 824, 857, 948, 971}

Mean of given numbers is:

`Mean = (Sum of all observations)/(Total number of observation)`

`=(136+ 238+ 320+ 403+ 434+ 553+ 555+  571+ 571+ 581+ 723+ 824+ 857+ 948+ 971)/(15)`

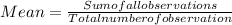
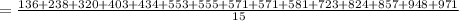
= 579

For finding Median, firstly we arrange data in ascending or descending order: 136, 238, 320, 403, 434, 553, 555, 571, 571, 581, 723, 824, 857, 948, 971

Here number of terms is 15 which is odd.

So, Median = { (n + 1) ÷ 2 }th term

= { (15 + 1) ÷ 2 }th term

=
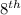`8^(th)` term

= 571

For finding mode, We see the observation that has maximum number of frequency.

Here 571 is repeated 2 times and its frequency is maximum.

So, Mode = 571

Range = Highest value - Lowest value

= 971 - 136

= 835

4. {136, 238, 320, 403, 434, 553, 555, 571, 571, 581, 723, 824, 857, 948, 971}

Mean of given numbers is:

`Mean = (Sum of all observations)/(Total number of observation)`

`=(208+ 226+ 323+ 433+ 433+ 489+ 574+ 594+ 599+ 803 803+ 803+ 875+ 951+ 969)/(15)`

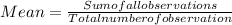
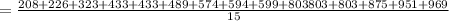
= 605.5333

For finding Median, firstly we arrange data in ascending or descending order: 208, 226, 323, 433, 433, 489, 574, 594, 599, 803, 803, 803, 875, 951, 969

Here number of terms is 15 which is odd.

So, Median = { (n + 1) ÷ 2 }th term

= { (15 + 1) ÷ 2 }th term

=
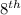`8^(th)` term

= 594

For finding mode, We see the observation that has maximum number of frequency.

Here 803 is repeated 3 times and its frequency is maximum.

So, Mode = 803

Range = Highest value - Lowest value

= 969 - 208

= 761