Question

Calculate the electric double layer thickness of a alumina colloid in a dilute (0.1 mol/dm3) CsCI electrolyte solution at 30 °C. How are these numbers affected by the addition of 0.1 mol/dm3 of KCL? At what distance from the particle surface (r) has the potential decayed to 1% of its initial value?

Answer 1

Step-by-step explanation:

The given data is as follows.

Concentration = 0.1
`mol/dm^(3)`

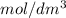
= 0.1 \frac{mol dm^{3}}{dm^{3}} \frac{10^{3}}{dm^{3}} \times \frac{6.022 \times 10^{23}}{1 mol} ions

=
`6.022 * 10^(25) ions/m^(3)`

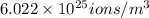
T =
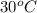`30^(o)C` = (30 + 273) K = 303 K

Formula for electric double layer thickness (
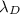`\lambda_(D)`) is as follows.

`\lambda_(D)` =
`(1)/(k) = \sqrt (\varepsilon \varepsilon_(o) K_(g)T)/(2 n^(o) z^(2) \varepsilon^(2))`

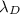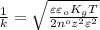
where,
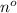`n^(o)` = concentration =
`6.022 * 10^(25) ions/m^(3)`

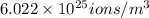
Hence, putting the given values into the above equation as follows.

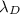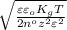
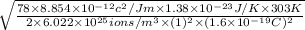
`\lambda_(D)` =
`\sqrt (\varepsilon \varepsilon_(o) K_(g)T)/(2 n^(o) z^(2) \varepsilon^(2))`

=
`\sqrt (78 * 8.854 * 10^(-12) c^(2)/Jm * 1.38 * 10^(-23)J/K * 303 K)/(2 * 6.022 * 10^(25) ions/m^(3) * (1)^(2) * (1.6 * 10^(-19)C)^(2))`

=
`9.669 * 10^(-10)` m

or, =
`9.7 A^(o)`

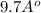
= 1 nm (approx)

Also, it is known that
`\lambda_(D)` =
`\sqrt (1)/(n^(o))`

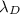Hence, we can conclude that addition of 0.1
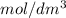`mol/dm^(3)` of KCl in 0.1
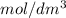`mol/dm^(3)` of NaBr "
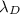`\lambda_(D)`" will decrease but not significantly.