Answer:
0.16 micron per day
Step-by-step explanation:
Given:
The initial crack length, a₁ = 0.1 micron = 0.1 × 10⁻⁶ m
Initial tensile stress, σ₁ = 120 MPa
Final stress = 30 MPa
now from Griffith's equation, we have
![\sigma=[(G_cE)/(\pi\ a)]^(1)/(2)](https://img.qammunity.org/2020/formulas/engineering/college/9v9d9eedpy01z4p41krnktm0rrb1vv273t.png)
where,
Gc and E are the material constants
now,
for the initial stage
![120=[(G_cE)/(\pi\ (0.1*10^(-6))]^(1)/(2)](https://img.qammunity.org/2020/formulas/engineering/college/2jpadqq4in8afb4y7iv4o22n6fmjwodb1v.png) ........{1}
........{1}
and for the final case
![30=[(G_cE)/(\pi\ a_2)]^(1)/(2)](https://img.qammunity.org/2020/formulas/engineering/college/hv20d49w7meyw5r0hg9snw14h9ispex1fx.png) ............{2}
............{2}
on dividing 1 by 2, we get
![(120)/(30)=[(a_2)/(0.1*10^(-6))]^(1)/(2)](https://img.qammunity.org/2020/formulas/engineering/college/1pgfrysr2bxyrlofs04nfxe7si2a15m860.png)
or
a₂ = 4² × 0.1 × 10⁻⁶ m
or
a₂ = 1.6 micron
Now,
the change from 0.1 micron to 1.6 micron took place in 10 days
therefore, the rate at which the crack is growing =
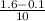
or
average rate of change of crack = 0.16 micron per day