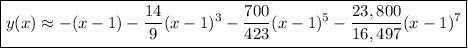We're set up to find a series solution to the ODE centered around
 . Let's first replace
. Let's first replace
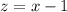 , so that
, so that
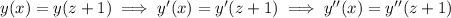
and we'll look for a series solution centered at
 . We have
. We have
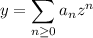
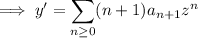
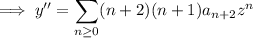
The ODE is then
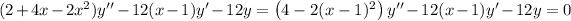
which in terms of
 is
is
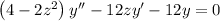
Substituting the series above into the ODE gives
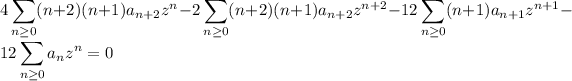
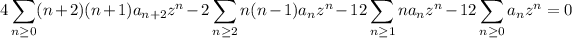
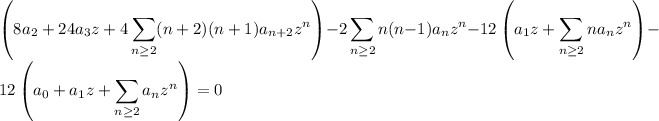
![\displaystyle(8a_2-12a_0)+(24a_3-24a_1)z+\sum_(n\ge2)\bigg[(4n^2+3n+2)a_(n+2)-(2n^2+10n+2)a_n\bigg]z^n=0](https://img.qammunity.org/2020/formulas/mathematics/college/qszxzhkf6nju7enkciqdkic606ectcewok.png)
so that the coefficients follow the recurrence,
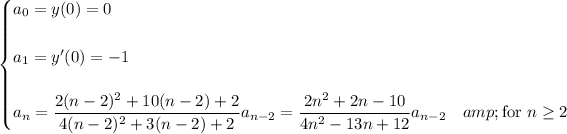
Thanks to the dependency between every other coefficient, we have
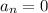 for all even-valued
for all even-valued
 . Meanwhile,
. Meanwhile,
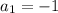
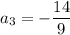
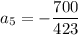
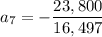
so that
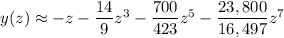
or in terms of
 ,
,