Answer:
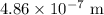
Step-by-step explanation:
R = Rydberg constant =
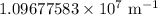
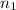 = Principal quantum number of an energy level = 2
= Principal quantum number of an energy level = 2
 = Principal quantum number of an energy level for the atomic electron transition = 4
= Principal quantum number of an energy level for the atomic electron transition = 4
Wavelength is given by the Rydberg formula

The wavelength of the light emitted is
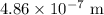 .
.