Answer: The energy released in the given nuclear reaction is 94.99 MeV.
Step-by-step explanation:
For the given nuclear reaction:
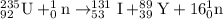
We are given:
Mass of
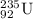 = 235.043924 u
= 235.043924 u
Mass of
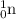 = 1.008665 u
= 1.008665 u
Mass of
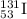 = 130.9061246 u
= 130.9061246 u
Mass of
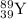 = 88.9058483 u u
= 88.9058483 u u
To calculate the mass defect, we use the equation:
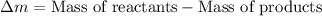
Putting values in above equation, we get:
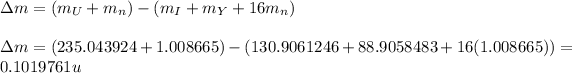
To calculate the energy released, we use the equation:
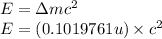
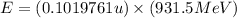 (Conversion factor:
(Conversion factor:
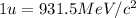 )
)
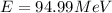
Hence, the energy released in the given nuclear reaction is 94.99 MeV.