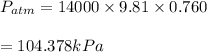Answer:
The atmospheric pressure is found to be
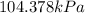
Step-by-step explanation:
We know that pressure exerted by a standing column of fluid is calculated using the equation
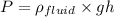
In our case the pressure of the standing column of mercury is equal to the atmospheric pressure.
According to the given data we have
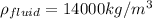
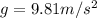
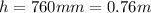
Using the values in the equation above we calculate atmospheric pressure to be