Question

A 2.5kg metal bar is quenched from 800°C by immersion in a closed insulated tank of water containing 50 litres of water initially at 20°C. Assuming that both water and the metal bar can be treated as incompressible, determine the final temperature of the metal bar and the water, whose specific heat capacities are 0.500 and 4.18 kJ/kg.K respectively, and hence, using Gibbs' equation, calculate the amount of entropy produced by the quenching process.

Answer 1

The amount of entropy produced by the quenching process is 0.303 kJ/K.

Step-by-step explanation:

Given that,

Mass = 2.5 kg

Temperature = 800°C

The mass of 50 L of water is 50 kg

Temperature = 20°C

Energy = 4.18 kJ/kg.K

If the final temperature of the metal bar and water is T₀°C, then

The heat lost by the bar = heat gained by water

`m_(w)C_(w)(T_(0)-T)=m_(B)c_(B)(T-T_(0))`

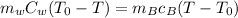
Put the value into the formula

`4.18*50(T-20)=0.5*2.5(80-T)`

`209T-4180=1000-1.25T`

`210.25T=5180`

`T=(5180)/(210.25)`

`T=24.64^(\circ)C`

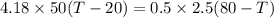
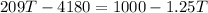
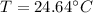
Now, heat exchange between the systems

`\Delta Q=m_(w)C_(w)(T-20)`

`\Delta Q=4.18*50(24.64-20)`

`\Delta Q=969.76\ kJ`

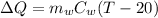
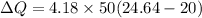
We need to calculate the entropy

Using formula of entropy

`S=(\Delta Q)/((T+T_(0))/(2)+T')-(\Delta Q)/((T+T_(0))/(2)+T')`

Where, T' = 273.15\ K

Put the value into the formula

`S=(969.76)/((20+24.64)/(2)+273.15)}-(969.76)/((80+24.64)/(2)+273.15)`

`S=3.28209293668-2.97956800934`

`S=0.303\ kJ/K`

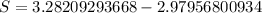
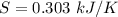
Hence, The amount of entropy produced by the quenching process is 0.303 kJ/K.