Answer: 693 years
Explanation:
Expression for rate law for first order kinetics is given by:

k = rate constant
t = time taken for decomposition = 1
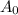 = Initial amount of the reactant
= Initial amount of the reactant
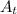 = amount of the reactant left =
= amount of the reactant left =
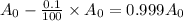

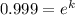

for half life :
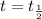
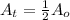
Putting in the values , we get
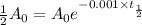
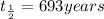
Thus half life of this isotope, to the nearest year is 693.