Answer:
Change in entropy is 0.8712 kJ/kgK
Given:
Initial Temperature, T = 320 K
Initial Pressure, P = 130 kPa
Final Pressure, P' = 438 kPa
Solution:
Here, a rigid tank is considered, therefore, the volume of the tank is constant and for a process at constant volume:
Pressur, P ∝ Temperature, T
Therefore,
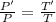

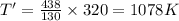
Now, change in entropy is given by:
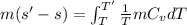
![(s' - s) = 0.718[ln(T')/(T)]_(320)^(1078)](https://img.qammunity.org/2020/formulas/engineering/college/l6t3dbzktokhs55vjciavpzdzfunghsl1r.png)
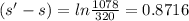
Therefore, change in entropy is 0.8712 kJ/kgK