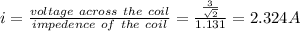Question

An oscillating RLC circuit consisting of a resistance of 10 ohms, a 1.0nF capacitor, and a 3.0 mH coil has a maximum voltage of 3.0 V. a. What is the impedance of the circuit if the oscillating frequency is 377 rad/s

b. What is the resonance frequency of this circuit?
c. If the maximum amplitude of the AC voltage source is 170 V
i. What is the maximum current through the circuit at the resonance condition?
ii. What is the voltage across the coil?

Answer 1

(A) 2652.49 ohm (b) 91937.45311 Hz (c) (i) 12.022 A (II) 2.324 A

Step-by-step explanation:

We have given resistance R = 10 ohm

Capacitance C = 1 nF

Inductance of the coil L = 3 mH

(A) Inductive reactance
`X_L=\omega L=377* 3* 10^(-3)=1.131ohm`

Capacitive reactance
`X_C=(1)/(\omega C)=(1)/(377* 10^(-9))=2.6525* 10^6ohm`

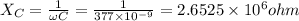
Impedance
`Z=√(R^2+(X_C-X_L)^2)=√(10^2+(2652500-1.131)^2)=2652.49ohm`

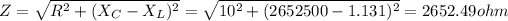
(b) We know that resonance frequency
`f=(1)/(2\pi √(LC))=\frac{1}{2\pi \sqrt{3* 10^(-3)* 10^(-9)}}=91937.45311Hz`

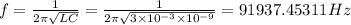
(c) (i) At resonance condition
`X_L=X_C` so only effective resistance is R

So maximum current
`i=(V)/(R)=((170)/(√(2)))/(10)=12.022A`

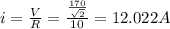
(ii) Current across the coil
`i=(voltage\ across\ the\ coil)/(impedence\ of\ the\ coil)=((3)/(√(2)))/(1.131)=2.324A`