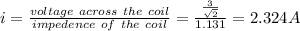Answer:
(A) 2652.49 ohm (b) 91937.45311 Hz (c) (i) 12.022 A (II) 2.324 A
Step-by-step explanation:
We have given resistance R = 10 ohm
Capacitance C = 1 nF
Inductance of the coil L = 3 mH
(A) Inductive reactance
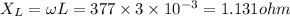
Capacitive reactance
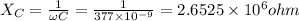
Impedance
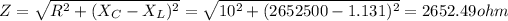
(b) We know that resonance frequency
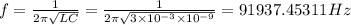
(c) (i) At resonance condition
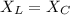 so only effective resistance is R
so only effective resistance is R
So maximum current
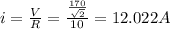
(ii) Current across the coil