Question

Each of the two coils has 320 turns. The average radius of the coil is 6 cm. The distance from the center of one coil to the electron beam is 3 cm. If a current of 0.5 amperes runs through the coils, what is the magnitude of the magnetic field at a location on the axis of the coils, midway between the coils

Answer 1

Magnetic field,
`B=2.39* 10^(-3)\ T`

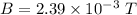
Step-by-step explanation:

It is given that,

Number of turns, N = 320

Radius of the coil, r = 6 cm = 0.06 m

The distance from the center of one coil to the electron beam is 3 cm, x = 3 cm = 0.03 m

Current flowing through the coils, I = 0.5 A

We need to find the magnitude of the magnetic field at a location on the axis of the coils, midway between the coils. The magnetic field midway between the coils is given by :

`B=(\mu_oINr^2)/((x^2+r^2)^(3/2))`

`B=(4\pi * 10^(-7)* 0.5* 320* (0.06)^2)/((0.03^2+0.06^2)^(3/2))`

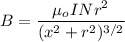
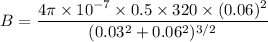
B = 0.00239 T

or

`B=2.39* 10^(-3)\ T`

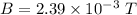
So, the magnitude of the magnetic field at a location on the axis of the coils, midway between the coils is
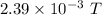`2.39* 10^(-3)\ T`. Hence, this is the required solution.