Answer:
The correct option is E.
Explanation:
It is given that Alice, Benjamin, and Carol each try independently to win a carnival game.
Let A, B and C represent the following events.
A = Alice win
B = Benjamin win
C = Carol win
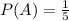 and
and
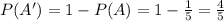
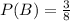 and
and
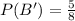
 and
and

We need to find the probability that exactly two of the three players will win but one will lose.
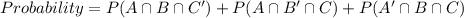
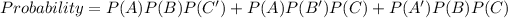
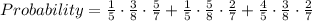


The probability that exactly two of the three players will win but one will lose is
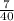 .
.
Therefore the correct option is E.