Question

c) If an initial investment of $ 35,000 grows to $257,000 in 15 years, what annual interest rate, continuously compounded, was earned?

Answer 1

Answer: 13.29%

Explanation:

The formula to calculate the compound amount (compounded continuously) is given by :-

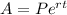`A=Pe^(rt)`, where P is the principal amount , r is the rate of interest ( in decimal) and t is the time period.

Given : P= $ 35,000 , A= $257,000 and t=15 years

To find : r , we substitute all the values in the above formula , we get

`257000=(35000)e^(15r)\\\\\Rightarrow\ e^(15r)=(257000)/(35000)\\\\\Rightarrow\ e^(15r)=7.3428`

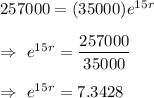
Taking natural log on both the sides , we get

`15r=\ln(7.3428)\\\\\Rightarrow\ 15r=1.9937\\\\\Rightarrow\ r=(1.9937)/(15)0.132913333333\approx0.1329=13.29\%`

Hence, the annual interest rate = 13.29%