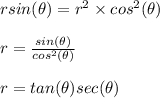Answer:
1) Thus point (3,4) is represented as (5,53
 ) in polar format.
) in polar format.
2) Polar form is
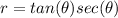
Explanation:
Any point (x,y) can be represented in polar format (r,θ) as
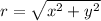
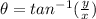
Using the above formula
The point (3,4) is represented in polar format as
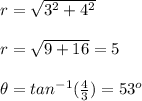
Thus point (3,4) is represented as (5,53
 )
)
2)
The given curve is
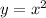
to convert it to polar form put
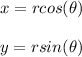
Thus the curve becomes