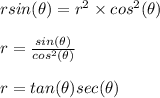Question

Find the polar coordinates for the point whose rectangular coordinates are (3,4). 6. Convert y x2 to polar form.

Answer 1

1) Thus point (3,4) is represented as (5,53
`^(o)`) in polar format.

2) Polar form is
`r=tan(\theta )sec(\theta)`

Explanation:

Any point (x,y) can be represented in polar format (r,θ) as

`r=\sqrt{x^(2)+y^(2)}`

`\theta =tan^(-1)((y)/(x))`

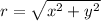
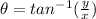
Using the above formula

The point (3,4) is represented in polar format as

`r=\sqrt{3^(2)+4^(2)}\\\\r=√(9+16)=5\\\\\theta =tan^(-1)((4)/(3))=53^(o)`

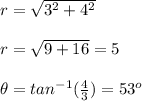
Thus point (3,4) is represented as (5,53
`^(o)`)

2)

The given curve is
`y=x^(2)`

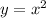
to convert it to polar form put

`x=rcos(\theta )\\\\y=rsin(\theta )`

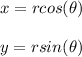
Thus the curve becomes

`rsin(\theta )=r^(2)* cos^(2)(\theta )\\\\r=(sin(\theta ))/(cos^(2)(\theta ))\\\\r=tan(\theta )sec(\theta)`