Question

Whats My number is????

Answer 1

The answer should be 91, 1 is 8 away from the tens digit which is 9!

Answer 2

Answer: The required number is 91.

Step-by-step explanation: Given that a number has a tens digit that is 8 more than the ones digit. Zero is not one of the digits.

We are to find the number.

Let x and y represents the digit in ten's place and one's place respectively.

So, the number is
`n=10x+y.`

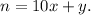
According to the given information, we have

`x=8+y.`

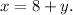
Therefore,w e get

`n=10x+y=10(8+y)+y=80+11y.`

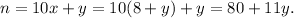
Since the number is of two digits and x, y are not zero, so the required value of y is 1.

That is, given number is

`n=80+11*1=91.`

Thus, the required number is 91.