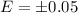Answer with explanation:
The confidence interval for population proportion is given by :_
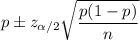
Where :
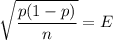 is the margin of error , n is the sample size , p is the sample proportion of success and
is the margin of error , n is the sample size , p is the sample proportion of success and
 is the significance level.
is the significance level.
Given : Confidence level :
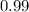
Then , Significance level :
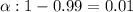
Sample size :
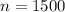
Sample proportion of respondents chose chocolate pie:
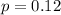
Margin of error :