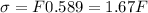Question

A circular tube AB is fixed at one end and free at the other end. The tube is subjected to axial force at joint B. If the outer diameter of the tube is 3 in. and the thickness is ¾ in., calculate the maximum normal stress in the tube.

Answer 1

Max. normal stress,
`\sigma = \farc{3}{0.589} = 1.67F ksi`

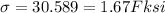
Given:

Outer diameter, d = 3 in

thickness, t =
`(3)/(4) in`

Solution:

Now, we know that in case of axial force, the normal stress is maximum, therefore:

Max. normal stress,
`\sigma = \farc{force, F }{Cross -sectional area, A}` (1)

The axial load is F kips (say)

Now, cross sectional area, A =
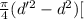`(\pi )/(4)(d'^(2) - d^(2))[` (2)

where

d = inner diameter

Now,

d = d' - 2t

d = 3 -
`2\fra{3}{4} = (3)/(2) in`

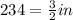
Now, using the value of 'd' in eqn (2):

A =
`(\pi )/(4)(3^(2) - ((3)/(2))^(2)) = 0.589 in^(2)`

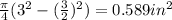
Now, using eqn (1):

Max. normal stress,
`\sigma = \farc{F}{0.589} = 1.67F`