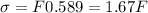Answer:
Max. normal stress,
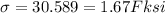
Given:
Outer diameter, d = 3 in
thickness, t =
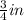
Solution:
Now, we know that in case of axial force, the normal stress is maximum, therefore:
Max. normal stress,
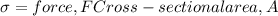 (1)
(1)
The axial load is F kips (say)
Now, cross sectional area, A =
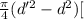 (2)
(2)
where
d = inner diameter
Now,
d = d' - 2t
d = 3 -
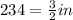
Now, using the value of 'd' in eqn (2):
A =
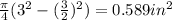
Now, using eqn (1):
Max. normal stress,