Answer:
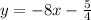
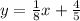
↓
The lines are perpendicular
Explanation:
If we have two lines of equations:
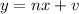 (1)
(1)
 (2)
(2)
Where n is the slope of the line (1) and m is the slope of the line (2)
Then by definition it is fulfilled that if
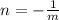 means that the lines (1) and (2) are perpendicular
means that the lines (1) and (2) are perpendicular
In this case the lines are:
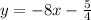 (1)
(1)
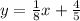 (2)
(2)
Observe that:
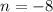 and
and
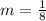
Then it is fulfilled that
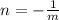 because:
because:
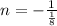
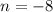
Therefore the lines are perpendicular