Answer:
After 0.24 hours Rahul and Kumi are closest to each other.
Explanation:
It is given that Rahul is 4 kilometers due south of the post office and traveling toward it at 10 kilometers per hour. It means length of leg1 after t hours is
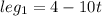
At noon, Kumi is 2 kilometers due east of the post office and jogging easy away from it at 5 kilometers per hour. It means length of leg2 after t hours is
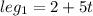
Using Pythagoras theorem,
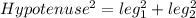
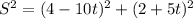
Differentiate with respect to t.
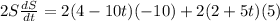
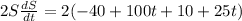
Cancel out common factors.
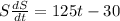
Divide both sides by S.
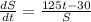
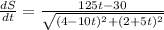 .... (1)
.... (1)
Equate
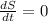 , to find critical values.
, to find critical values.
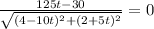
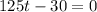
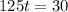
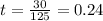
The critical value of the distance function is 0.24.
Differentiate (1) with respect to t.
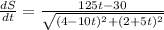
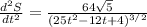
Substitute t=0.24,
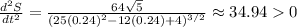
Since
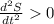 , therefore the distance of Rahul and kumi is minimum at t=0.24.
, therefore the distance of Rahul and kumi is minimum at t=0.24.
Therefore, after 0.24 hours Rahul and Kumi are closest to each other.