Question

At noon, Rahul is 4 kilometers due south of the post office and traveling toward it at 10 kilometers per hour. Also at noon, Kumi is 2 kilometers due east of the post office and jogging easy away from it at 5 kilometers per hour. After how many hours will they be closest to each other?

Answer 1

After 0.24 hours Rahul and Kumi are closest to each other.

Explanation:

It is given that Rahul is 4 kilometers due south of the post office and traveling toward it at 10 kilometers per hour. It means length of leg1 after t hours is

`leg_1=4-10t`

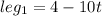
At noon, Kumi is 2 kilometers due east of the post office and jogging easy away from it at 5 kilometers per hour. It means length of leg2 after t hours is

`leg_1=2+5t`

Using Pythagoras theorem,

`Hypotenuse^2=leg_1^2+leg_2^2`

`S^2=(4-10t)^2+(2+5t)^2`

Differentiate with respect to t.

`2S(dS)/(dt)=2(4-10t)(-10)+2(2+5t)(5)`

`2S(dS)/(dt)=2(-40+100t+10+25t)`

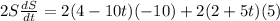
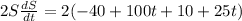
Cancel out common factors.

`S(dS)/(dt)=125t-30`

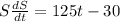
Divide both sides by S.

`(dS)/(dt)=(125t-30)/(S)`

`(dS)/(dt)=(125t-30)/(√((4-10t)^2+(2+5t)^2))` .... (1)

Equate
`(dS)/(dt)=0`, to find critical values.

`(125t-30)/(√((4-10t)^2+(2+5t)^2))=0`

`125t-30=0`

`125t=30`

`t=(30)/(125)=0.24`

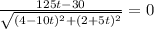
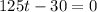
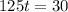
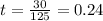
The critical value of the distance function is 0.24.

Differentiate (1) with respect to t.

`(dS)/(dt)=(125t-30)/(√((4-10t)^2+(2+5t)^2))`

`(d^2S)/(dt^2)=(64 √(5))/((25 t^2 - 12 t + 4)^(3/2))`

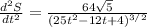
Substitute t=0.24,

`(d^2S)/(dt^2)=(64 √(5))/((25 (0.24)^2 - 12 (0.24) + 4)^(3/2))\approx 34.94>0`

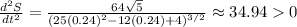
Since
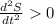`(d^2S)/(dt^2)>0`, therefore the distance of Rahul and kumi is minimum at t=0.24.

Therefore, after 0.24 hours Rahul and Kumi are closest to each other.