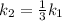Question

A spring-mass system with k1 and m has a natural frequency of ωn. If a second spring k2 is added in series with the first spring, the natural frequency is lowered to 1/2*wn. Determine k2 in terms of k1.

Answer 1

`k_(2) = (1)/(3)k_(1)`

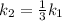
Solution:

Natural frequency of a spring mass system is given by:

`\omega = \sqrt{(k)/(m)}` (1)

Now, with a system with
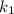`k_(1)` and mass m, natural frequency is:

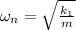`\omega_(n) = \sqrt{(k_(1))/(m)}` (2) (given)

Also, when another spring
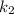`k_(2)` is added in series with the first one the natural frequency of the system reduces to
`(\omega_(n))/(2)`, spring's equivalent stiffness is given by:

`(1)/(k_(eq))= (1)/(k_(1)) + (1)/(k_(2))`

`k_(eq) = (k_(1)k_(2))/(k_(1) + k_(2))`

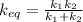
Therefore,

`(\omega_(n))/(2) = \sqrt{(k_(eq))/(m)}`

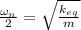
`\omega_(n) = 2\sqrt{(k_(eq))/(m)}` (3)

From eqn (2) and (3):

`\sqrt{(k_(1))/(m)} = 2\sqrt{(k_(eq))/(m)}`

`\sqrt{(k_(1))/(m)} = 2\sqrt{(k_(1)k_(2))/(m(k_(1) + k_(2)))}`

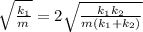
Squaring both sides of the above eqn, we get:

`(k_(1))/(m) = 4(k_(1)k_(2))/(m(k_(1) + k_(2)))`

`k_(1)^(2) = 4k_(1)k_(2) - k_(1)k_(2) = 0`

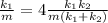
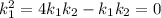
Solving the above equation in order to get the relation between
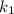`k_(1)` and
`k_(2)`:

`k_(1) = 3k_(2)`

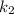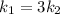
Therefore,
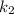`k_(2)` in terms of
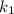`k_(1)`:

`k_(2) = (1)/(3)k_(1)`

Answer 2

`K_2=(K_1)/(3)`

Step-by-step explanation:

When only one spring is connected with mass

`\omega _n=\sqrt{(K_1)/(m)}`

When another spring is added in series with spring one ,then the equivalent spring constant is K

Given that final natural frequency become half

`\omega_f=\sqrt{(K)/(m)}`

`\omega_f=(1)/(2)\omega _n`

`K=(1)/(4)K_1` -----(1)

We know that equivalent spring constant for series connection is given as

`K=(K_1K_2)/(K_1+K_2)` -----(2)

By using equation 1 and 2 we can say that

`K_2=(K_1)/(3)`