Question

Identify the initial and final states (n; and nf) if an electron in hydrogen emits a photon with a wavelength of 4.103 x 10-7 m. ni=6 2 nf

Answer 1

The initial state is 6 and the final state is 2.

Step-by-step explanation:

Given, wavelength of photon,
`\lambda =4.103* 10^(-7) m`

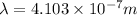
and the value of Plank's constant,
`h=6.626* 10^(-34) m^(2)kg/s`

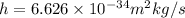
and the velocity of light,
`c=3* 10^(8) m/s`

And,
`1eV=1.6*10^(-19) J`

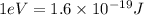
According to the Bohr model the nth level of electron will be,

`E_(n) =(-13.6)/(n^(2) ) eV`

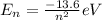
In the emission the energy is ejected out so,

`-\Delta E=E_(ni)-E_(nf)  \\-\Delta E=-13.6((1)/(n_(i) ^(2)  )-(1)/(n_(f) ^(2)  ) )eV`

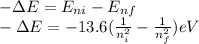
And the change in energy also,

`\Delta E=(hc)/(\lambda )`

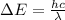
Equate above two values.

`(hc)/(\lambda )=-13.6((1)/(n_(i) ^(2)  )-(1)/(n_(f) ^(2)  ) )eV`

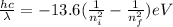
Therefore,

`(1)/(n_(i) ^(2) ) -(1)/(n_(f) ^(2) )=-(hc)/(\lambda (13.6 eV))`

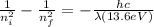
Put all the variables in the above equation

`(1)/(n_(i) ^(2) ) -(1)/(n_(f) ^(2) )=-(6.626* 10^(-34)(c=3* 10^(8) ))/(13.6(4.103* 10^(-7))(1.6*10^(-19) ) \\(1)/(n_(i) ^(2) ) -(1)/(n_(f) ^(2) )=0.22`

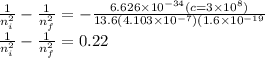
Now by putting the value of ni=6 and nf=2 to check the equality of equation.

`(1)/(2^(2) ) -(1)/(6^(2) )=0.22`

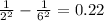
By looking at the above the value of ni=6 and nf=2 will satisfy the equation.