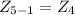Answer with step by step explanation:
We are given that a set
Let A={1,2,3,4}
We have to prove that it is a group under modulo 5
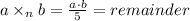
Closed property:
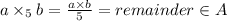 for all a,b belongs to A
for all a,b belongs to A
Associative property:It is satisfied property
 for all a,b,c belongs to A
for all a,b,c belongs to A
Identity :
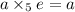 Where e is identity of group
Where e is identity of group
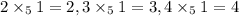
Hence, identity exist ,e=1
Inverse:
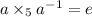

Hence, inverse exist of every element
Given set satisfied all properties of group under multiplication modulo.Therefore, givens set is a group under multiplication modulo.
It is a U(5) because a group under multiplication modulo is called U(n) group U(n)={r, gcd(r,n)=1}
We know that order of group U(n)=
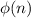
Order of U(5)=4
We know that
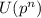 isomorphic to
isomorphic to
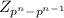
p=5,n=1
U(5)isomorphic to